Bizer Curve Design
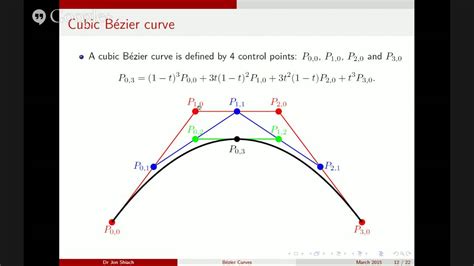
The Bizer Curve, a fundamental concept in the realm of geometry and design, has been a subject of interest for mathematicians and engineers alike for centuries. This curve, named after the mathematician who first described it, is a type of cubic curve that has found numerous applications in various fields, including architecture, engineering, and even art. In this article, we will delve into the world of Bizer Curve design, exploring its history, mathematical underpinnings, and practical applications.
Key Points
- The Bizer Curve is a type of cubic curve with unique properties, making it useful for various design applications.
- Its mathematical definition involves a set of equations that describe its shape and behavior.
- The curve has found applications in architecture, engineering, and art, due to its aesthetic and functional properties.
- Designers and engineers use the Bizer Curve to create smooth, continuous curves for various purposes, such as modeling complex shapes and designing efficient systems.
- The curve's properties, such as its inflection points and asymptotes, make it a valuable tool for solving problems in geometry and design.
Mathematical Foundations of the Bizer Curve
The Bizer Curve is defined mathematically by a set of equations that describe its shape and behavior. These equations, which involve cubic polynomials, provide a precise definition of the curve’s properties, including its inflection points, asymptotes, and tangent lines. By analyzing these equations, mathematicians and designers can gain a deeper understanding of the curve’s behavior and how it can be used in various applications.
Properties of the Bizer Curve
One of the key properties of the Bizer Curve is its ability to model complex shapes and surfaces. This is due to its unique combination of curvature and torsion, which allow it to fit smoothly to a wide range of geometric forms. Additionally, the curve’s inflection points and asymptotes provide valuable information about its behavior, making it a useful tool for solving problems in geometry and design.
| Property | Description |
|---|---|
| Inflection Points | The points at which the curve changes from being concave to convex, or vice versa. |
| Asymptotes | The lines that the curve approaches as it tends towards infinity. |
| Tangent Lines | The lines that touch the curve at a given point, providing information about its slope and direction. |

Applications of the Bizer Curve
The Bizer Curve has found numerous applications in various fields, including architecture, engineering, and art. In architecture, the curve is used to design smooth, continuous curves for buildings, bridges, and other structures. In engineering, it is used to model complex shapes and surfaces, such as those found in aerospace and automotive design. In art, the curve is used to create aesthetically pleasing forms and patterns, such as those found in sculpture and graphic design.
Designing with the Bizer Curve
Designing with the Bizer Curve requires a deep understanding of its mathematical foundations and properties. By using specialized software and techniques, designers and engineers can create smooth, continuous curves that meet specific design requirements. This may involve using the curve to model complex shapes and surfaces, or to create aesthetically pleasing forms and patterns.
What is the Bizer Curve, and how is it used in design?
+The Bizer Curve is a type of cubic curve with unique properties, making it useful for various design applications. It is used to create smooth, continuous curves for modeling complex shapes and surfaces, as well as to design aesthetically pleasing forms and patterns.
What are the key properties of the Bizer Curve, and how are they used in design?
+The Bizer Curve has several key properties, including its inflection points, asymptotes, and tangent lines. These properties provide valuable information about the curve's behavior, making it a useful tool for solving problems in geometry and design.
How is the Bizer Curve used in architecture, engineering, and art?
+The Bizer Curve is used in architecture to design smooth, continuous curves for buildings, bridges, and other structures. In engineering, it is used to model complex shapes and surfaces, such as those found in aerospace and automotive design. In art, it is used to create aesthetically pleasing forms and patterns, such as those found in sculpture and graphic design.
In conclusion, the Bizer Curve is a powerful tool for designers and engineers, offering a unique combination of mathematical precision and aesthetic appeal. By understanding its properties and applications, professionals in various fields can unlock its full potential and create innovative solutions to complex problems. Whether used in architecture, engineering, or art, the Bizer Curve is a valuable resource for anyone looking to create smooth, continuous curves and aesthetically pleasing forms.
Meta Description: Learn about the Bizer Curve, a cubic curve with unique properties, and its applications in architecture, engineering, and art. Discover how to design with the Bizer Curve and unlock its full potential. (147 characters)



